链表
链表
哈希表简单介绍

有序表简单介绍
时间复杂度O(logN)

链表
链表中的常见做题技巧主要有两类
一类是借助额外空间复杂度来帮助我们解决问题,比如借助哈希表、数组等,这种技巧主要用于笔试快速做题。
另一类是用于面试体现自己算法能力的,比如快慢指针。
反转链表
可能需要返回值换“头”
//单链表
public static Node reverse(Node header){
Node pre = null;
Node next = null;
while(header != null){
next = header.next;
header.next = pre;
pre = header;
header = next;
}
return pre;
}
//双链表
public static Node Doublereverse(DoubleNode header){
DoubleNode pre=null;
DoubleNode next=null;
while(head != null){
next=header.next;
header.next=pre;
header.last=next;
pre=header;
header=next;
}
return pre;
}打印公共部分
类似归并排序,两个链表均为有序链表
public static void sameprint(Link a,Link b){
Node aheader=a.header;
Node bheader=b.header;
while(aheader!=null && bheader!=null){
if(aheader.data < bheader.data){
aheader=aheader.next;
}else if(aheader.data > bheader.data){
bheader=bheader.next;
}else{
System.out.println(aheader.data);
aheader=aheader.next;
bheader=bheader.next;
}
}
}回文判断
暴力实现
暴力思路:直接利用栈,将每个数放入栈中,根据先进后出的特点,同时从头开始遍历链表,链表指针指向一个数同时让栈弹出一个数,看是否匹配,不匹配则不是
/**
* 借助栈判断回文链表
* 时间复杂度O(n),需要的额外空间复杂度为O(n)
* @param head
* @return
*/
public static boolean isPalindromeListByStack1(Node head) {
Stack<Node> nodeStack = new Stack<Node>();
Node node = head;
while(node != null) {
nodeStack.push(node);
node = node.next;
}
node = head;
while (node != null) {
if(node.value != nodeStack.pop().value) {
return false;
}
node = node.next;
}
return true;
}优化:只将后半部分的数据放入栈中,需要利用快慢指针,来实现这个功能
快指针每次走两步,慢指针每次走一步,快指针走完后,慢指针在中点,这个功能一定要多写Code,各种特殊定制慢指针位置,以及在链表长度为1,2,3这种特殊短链表也有预期效果
快慢指针
偶数个快指针从2开始比3开始多右移一次,1和2一样
奇数个从2和3开始一样,1开始多一次==
- 如果链表个数是奇数个,返回中点,如果链表个数是偶数个,返回上中点
- 如果链表个数是奇数个,返回中点,如果链表个数是偶数个,返回下中点
- 如果链表个数是奇数个,返回中点,如果链表个数是偶数个,返回上中点前一
- 如果是奇数个返回中点的前一个结点,偶数个则返回上中点
/**
* 如果链表个数是奇数个,返回中点,如果链表个数是偶数个,返回上中点
* @param head
* @return
*/
public static Node midOrUpMidNode(Node head) {
// 当链表为空直接返回空(node),或者长度为1和2时,返回头结点即为中点
if(head == null || head.next == null || head.next.next == null) {
return head;
}
// 慢指针
Node slow = head.next;
// 快指针
Node fast = head.next.next;
whille(fast.next != null && fast.next.next != null){
fast=fast.next.next;
slow=slow.next;
}
return slow;
}
/**
* 如果链表个数是奇数个,返回中点,如果链表个数是偶数个,返回下中点
* @param head
* @return
*/
public static Node midOrUpDownNode(Node head) {
// 当链表为空直接返回空(node),或者长度为1和2时,返回头结点即为中点
if(head == null || head.next == null || head.next.next == null) {
return head;
}
// 慢指针
Node slow = head.next;
// 快指针,主要这里一开始少next一次,让slow在偶数次情况时多走一步,从而到达下中点
Node fast = head.next;
while(fast.next != null && fast.next.next!=null){
fast=fast.next.next;
slow=slow.next;
}
/**
* 容器法判断回文优化法
* 通过找中点减少 n/2 的额外空间消耗
* 奇数中点下一个,偶数下中点
* @param head
* @return
*/
public static boolean isPalindromeListByStack2(Node head) {
Stack<Node> nodeStack = new Stack<Node>();
if(head==null || head.next==null){
return true;
}
Node fast = head;
Node slow = head.next;
while(fast != null || fast.next != null || fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
}
while (slow != null) {
nodeStack.push(slow);
slow = slow.next;
}
Node node = head;
while(!nodeStack.isEmpty()) {
if(node.value != nodeStack.pop().value) {
return false;
}
}
return true;
}额外空间复杂度O(1)的方式
//慢指针到中点后,将后半部分逆序,然后依次比对,最后将后半部分恢复
/**
* 通过改原链表的方法判断回文链表
* 时间复杂度O(n),空间复杂度O(1)
* @param head
* @return
*/
public static boolean isPalindromeList3(Node head) {
// 没有结点或者一个结点默认是回文链表
if(head == null || head.next == null) {
return true;
}
// 找链表中点位置(奇数找中点,偶数找上中点或下中点,这里以上中点为例)
// n1是快慢指针中的慢指针,n2则是快指针,这里为了变量复用就不定义为fast和slow了
Node n1 = head;
Node n2 = head;
while(n2.next != null || n2.next.next != null) {
n2 = n2.next.next;
n1 = n1.next;
}
// 此时n1指向中点/上中点,找到中点后进行将中点后链表逆序的操作
// 将n2指向中点下一个结点
n2 = n1.next;
// 将中点指向null,方便后期判断链表是否校验完毕
n1.next = null;
// 引入新变量 n3,辅助逆转中点后链表
Node n3 = null;
while (n2 != null) {
// 用n3保存n2的下一结点
n3 = n2.next;
// 将n2指针向前指
n2.next = n1;
// 将n1、n2向后移动,继续逆转链表
n1 = n2;
n2 = n3;
}
// 此时n1指向逆转后的链表的尾节点
// 逆转后的链表是这种形式的:x->x->x<-x<-x
// 之后我们要从左右两端结点出发判断回文
// 为了节省变量,依然使用之前定义好的
// 注意要保留一个指向尾节点的指针方便之后恢复链表
n3 = n1;
// n2指向头结点
n2 = head;
// 定义一个返回结果变量
boolean res = true;
while(n1 != null && n2 != null) {
if(n1.value != n2.value) {
res = false;
break;
}
// n1从左到右
n1 = n1.next;
// n2从右到左
n2 = n2.next;
}
// 最后要将链表恢复原样,做法和逆转时相同,是逆转操作的反过程
n1 = n3.next;
n3.next = null;
while(n1 != null) {
n2 = n1.next;
n1.next = n3;
n3 = n1;
n1 = n2;
}
return res;
}左边中间右边
按值划分左中右
暴力思路
把链表放入数组中,在数组中做partition (笔试用)
基本思想就是快排中作为划分函数的荷兰国旗问题,将链表放到数组中然后做荷兰国旗划分,示例代码如下
/**
* 划分链表-解法一,借助荷兰国旗问题思想将链表放到数组中划分
* @param head 链表的头结点
* @param pivot 划分值
* @return
*/
public static Node listPartition1(Node head, int pivot) {
if(head == null) {
return head;
}
// 链表长度
int n = 0;
// 临时指针变量
Node node = head;
// 计算出链表长度
while (node != null) {
n++;
node = node.next;
}
// 定义出存放链表的数组
Node[] nodes = new Node[n];
// 将链表按序放入数组
int i = 0;
node = head;
while(node != null) {
nodes[i++] = node;
node = node.next;
}
// 借助荷兰国旗问题的划分函数进行划分
partition(nodes, pivot);
// 划分完成后记得将数组中的结点串起来形成新的链表,并返回其头结点
for(i = 0; i < nodes.length - 1; i++) {
nodes[i].next = nodes[i + 1];
}
nodes[n - 1].next = null;
return nodes[0];
}
/**
* 荷兰国旗问题划分函数
* 将原数组按照传入的pivot基准值划分,效果为:小于区域,等于区域,大于区域
* @param nodes
* @param pivot
*/
public static void partition(Node[] nodes, int pivot) {
// 小于区域右边界下标
int less = -1;
// 大于区域左边界下标
int more = nodes.length;
// 游标
int index = 0;
// 进行划分
while (index < more) {
if(nodes[index].value < pivot) {
// 如果当前结点值小于划分值,当前结点和小于区域右侧结点交换,小于区域向右扩
swap(nodes, ++less, index++);
} else if(nodes[index].value == pivot) {
// 如果当前结点等于划分值,等于区域向右扩,其他两个区域不变
index++;
} else {
// 如果当前结点值大于划分值,当前结点和大于区域左侧结点交换,大于区域向左扩
swap(nodes,--more,index++);
}
}
}
/**
* 交换函数
* @param nodes
* @param a
* @param b
*/
public static void swap(Node[] nodes, int a, int b) {
Node temp = nodes[a];
nodes[a] = nodes[b];
nodes[b] = temp;
}优化思想
题目给定链表头结点和划分值,定义6个变量即6个指针,分别代表小于区域头部(以下简称小头,其他变量含义类似)小尾,等头等尾,大头大尾。
然后遍历一遍链表将其拆散到三个区域上并通过各个区域的头尾指针记录好三个区域的链表,形成三个链表,最后再将三个链表合并。
注意:有可能三个部分有为空的部分
public static Node listPartition2(Node head,int pivot){
Node sH = null;
Node sT = null;
Node eH = null;
Node eT = null;
Node bH = null;
Node bT = null;
Node next=null;
while(head != null){
next = head.next;
head.next = null;
if (head.value < pivot){
if (sH == null){
sH = head;
sT = head;
} else {
sT.next = head;
sT = head;
}
}else if(head.value == pivot){
if (eH == null){
eH = head;
eT = head;
} else {
eT.next = head;
eT = head;
}
}else{
if (bH == null){
bH = head;
bT = head;
} else {
bT.next = head;
bT = head;
}
}
head = next;
}
// 将三个区域链表进行合并,需要考虑某个链表为空的情况
// 如果小于区域不为空,先从小于区域开始
if(sT != null) {
// 将小于区域尾和等于区域头相接
sT.next = eH;
// 谁去连大于区域的,谁变成eT
eT = eT == null ? sT : eT;
}
// 如果等于区域不为空
if(eH != null) {
// 将等于区域尾和大于区域头相接(大于区域有可能为空)
eT.next = bH;
}
// 不用继续判断大于区域为空的情况
// 从左到右判断三个区域的头,返回存在的那个
return sH != null ? sH : ( eH != null ? eH : bH);
}
}含有随机指针的链表
暴力思路
哈希表
用HashMap存结点,KV对为<老结点,老结点对应的克隆结点>,两次遍历链表,一次遍历生成老结点对应的克隆结点并把对应信息存到 map,再一次遍历设置好克隆结点的 next 和 random 指针,示例代码如下:
/**
* 带随机指针的链表结点
*/
public static class Node {
public int value;
public Node next;
public Node random;
public Node(int value) {
this.value = value;
this.next = null;
this.random = null;
}
}
/**
* 容器法-笔试用
* @param head
* @return
*/
public static Node copyRandomList1(Node head) {
if(head == null) {
return head;
}
HashMap<Node, Node> map = new HashMap<>();
Node node = head;
// 第一次遍历生成拷贝结点并将新老结点的对应信息存到map中
while(node != null) {
map.put(node, new Node(node.value));
node = node.next;
}
// 第二次遍历设置拷贝结点的next和random指针
node = head;
while(node != null) {
map.get(node).next = map.get(node.next);
map.get(node).random = map.get(node.random);
node = node.next;
}
// 返回拷贝链表的头结点
return map.get(head);
}优化思路
- 第一步:生成克隆节点,克隆节点放在原链表的next位置
- 第二步:一对一对拿出来
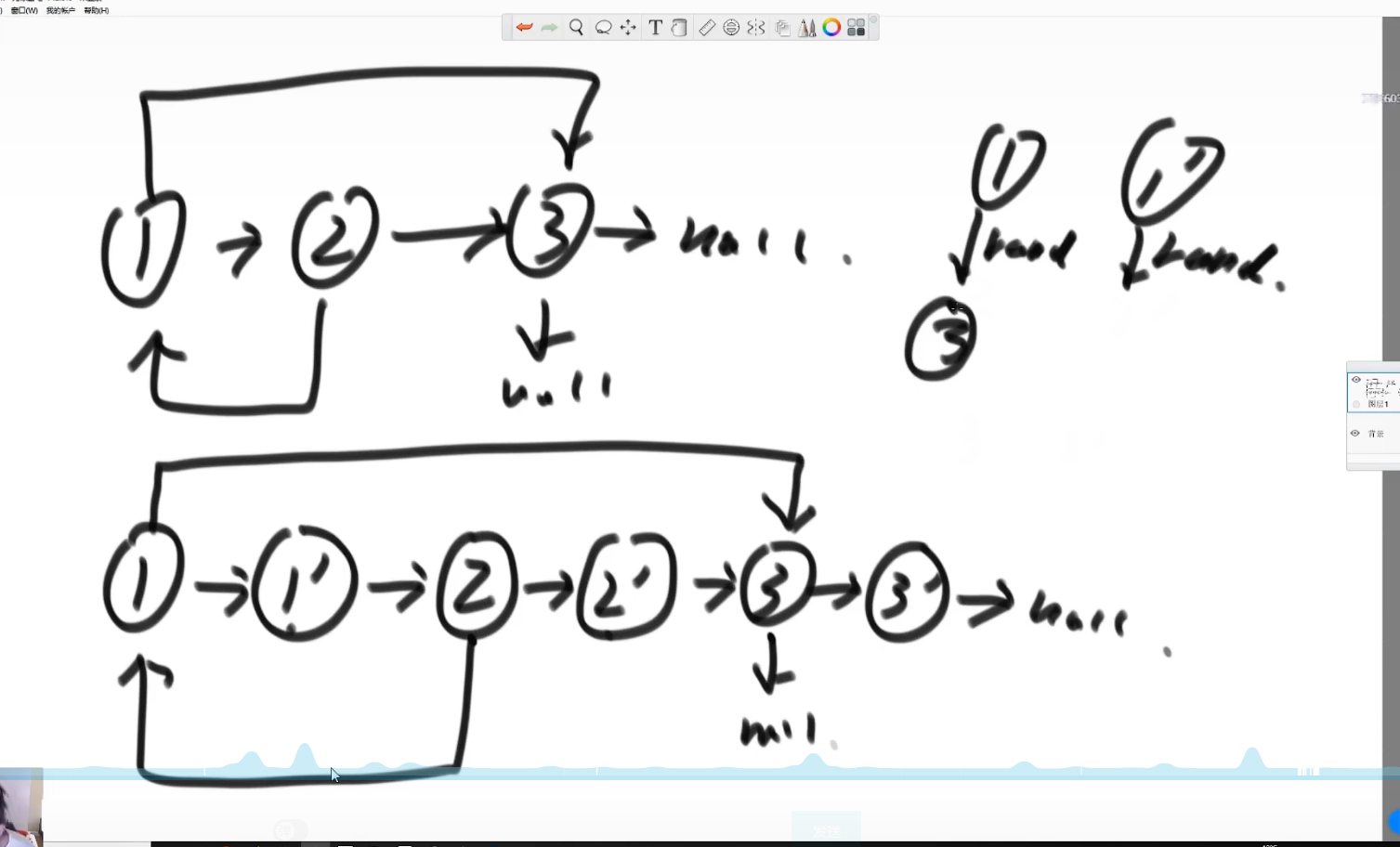
public static Node copyRandomList1(Node head) {
if (head == null){
return null;
}
// 第一步:生成克隆结点并穿插到原链表中
Node node = head;
Node next = null;
while(node != null) {
next = node.next;
node.next = new Node(node.value);
node.next.next = next;
node = next;
}
// 第二步:设置好克隆结点的random指针
Node copy = null;
node = head;
while(node != null) {
copy = node.next;
copy.random = node.random == null ? null : node.random.next;
node = node.next.next;
}
// 第三步:将拷贝结点从老链表中分离,并返回克隆链表
Node res = head.next;
node = head;
while(node != null) {
next = node.next.next;
copy = node.next;
copy.next = copy.next == null ? null : copy.next.next;
node.next = next;
node = next;
}
return res;
}
}带环的链表相交问题
问题描述:给定两个可能有环也可能无环的单链表,请实现如果两个链表相交,,返回相交的第一个结点,如果不相交,返回 null。
解题思路:
分两步
第一步:先判断环以及有环的话找到第一个入环结点
这一步依然是有两种解法:
1.容器法(笔试用)
容器法非常简单,用 HashSet 判重即可,示例代码如下:
/**
* HashSet判重找环
*
* @param head
* @return
*/
public static Node getLoopNodeBySet(Node head) {
if (head == null) {
return null;
}
HashSet<Node> set = new HashSet<>();
while (head != null) {
if (set.contains(head)) {
return head;
}
set.add(head);
head = head.next;
}
return null;
}2.不用容器,快慢指针(面试用)
快慢指针找环入口太经典了,总结就下面这三点:
- 快指针每次走两步,慢指针走一步,如果快指针到null则无环
- 如果有环,快慢指针会在环上相遇
- 相遇时,快指针回到开头,慢指针留原地,同时走一步,最后在第一个入环结点相遇
- 证明参考:(4条消息) leetcode142 环形链表解析和追及证明_大桑树保安队的博客-CSDN博客_leetcode142
/**
* 快慢指针判断链表是否有环以及找第一个入环结点
* 如果有环返回第一个入环结点,无环返回null
* @param head
* @return
*/
public static Node getLoopNode(Node head) {
if(head == null || head.next == null || head.next.next == null) {
return null;
}
Node fast = head.next.next;
Node slow = head.next;
while(fast != slow) {
if(fast == null) {
return null;
}
System.out.println(fast.data);
System.out.println(slow.data);
fast = fast.next.next;
slow = slow.next;
}
fast = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return fast;
}第二步:找环后分多种情况
(1)两个链表为空或都无环
两个链表一者为空说明没交点
两个链表不为空都无环的话,如果两个链表尾结点地址不同,说明没相交。
链表尾结点地址相同的话,用双指针找相交点,长的那个先走直到剩余长度和短的持平,最后两个指针一起走直到找到相交位置
/**
* 在两个链表都无环的情况下检查两个链表是否相交
* @return
*/
public static Node noLoop(Node head1, Node head2) {
if(head1 == null || head2 == null) {
return null;
}
// 一个细节点,用一个变量表示两链表长度的差值,从而节省一个变量
int n = 0;
Node node1 = head1;
Node node2 = head2;
while(node1 != null) {
n++;
node1 = node1.next;
}
while (node2 != null) {
n--;
node2 = node2.next;
}
// 如果尾结点不是同一个,不不相交
if(node1 != node2) {
return null;
}
// 双指针法找相交点
// 默认node1是较长链表
node1 = n > 0 ? head1 : head2;
node2 = node1 == head1 ? head2 : head1;
n = Math.abs(n);
while (n > 0) {
node1 = node1.next;
n--;
}
while(node1 != node2) {
node1 = node1.next;
node2 = node2.next;
}
return node1;
}(2) 一个有环、一个无环
这种情况不可能相交,一个有环和他相交的链表必定有环,这种情况直接返回null
(3) 两个链表都有环
如果两个链表都有环又分为三种情况:
- 两个链表完全不相交
- 两个链表的第一个入环结点相同,相交点可能在环外也可能在第一个入环结点上,其实就相当于不带环找相交位置,用双指针法即可
- 两个链表的第一个入环结点不同,判断两个链表入环结点是否都在一个环上,是的话相交返回其中一个入环结点,否则不相交
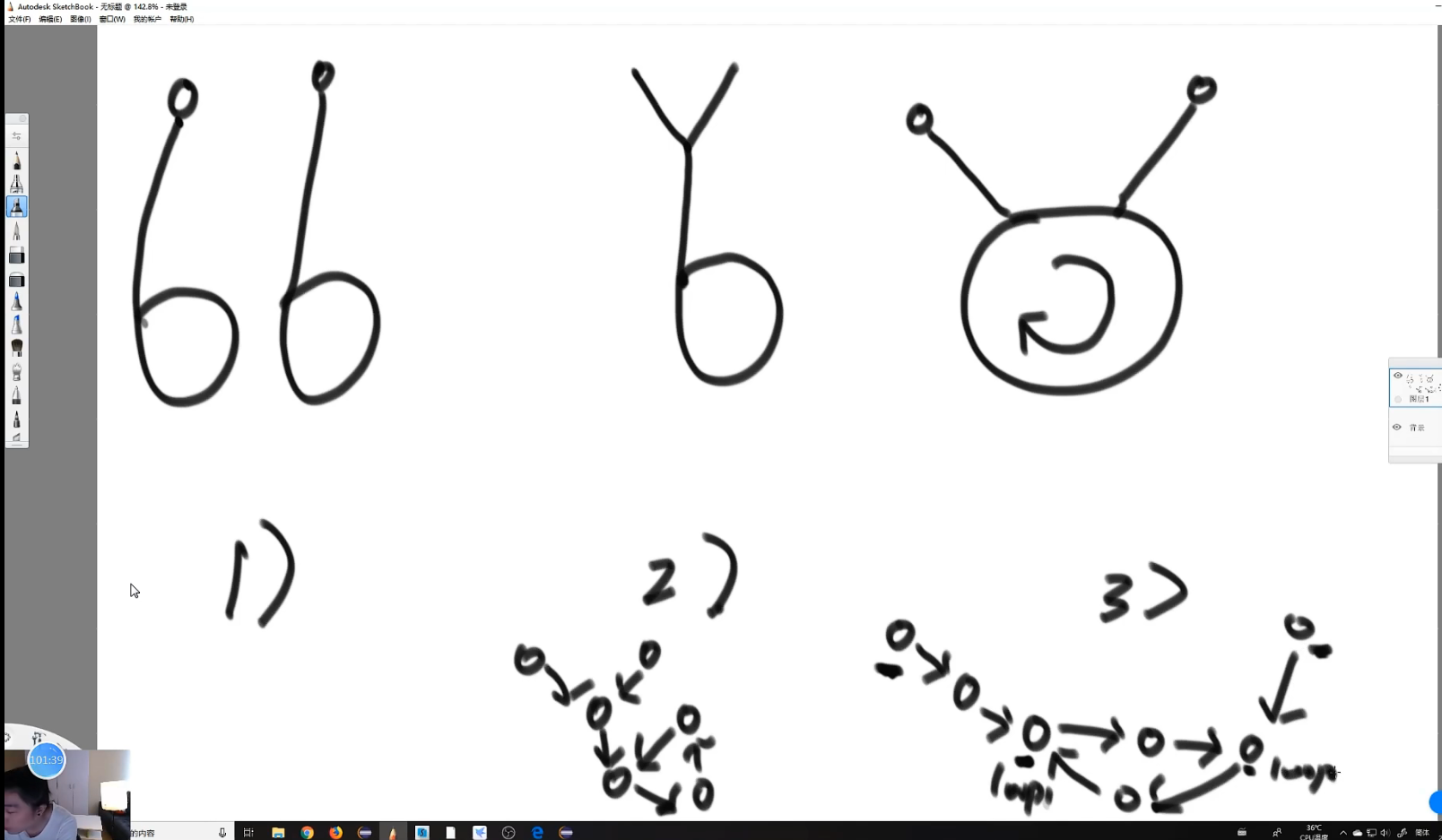
/**
* 两个链表都有环的情况
* @param head1
* @param loop1
* @param head2
* @param loop2
* @return
*/
public static Node bothHasLoop(Node head1, Node loop1, Node head2, Node loop2) {
Node node1 = null;
Node node2 = null;
// 如果两个链表第一个入环结点相同
if(loop1 == loop2) {
// 其实就相当于两个不带环的链表找相交位置,双指针法即可
//代码复用
int n = 0;
node1 = head1;
node2 = head2;
while(node1 != loop1) {
n++;
node1 = node1.next;
}
while(node2 != loop2) {
n--;
node2 = node2.next;
}
node1 = n > 0 ? head1 : head2;
node2 = node1 == head1 ? head2 : head1;
n = Math.abs(n);
while (n > 0) {
node1 = node1.next;
n--;
}
while (node1 != node2) {
node1 = node1.next;
node2 = node2.next;
}
return node1;
} else {
// 如果两个链表的入环结点不相同,判断两个入环结点是否在同一环上
// 如果在的话说明两个环相交,返回其中一个入环结点,否则不相交
node1 = loop1.next;
while (node1 != loop1) {
if(node1 == loop2) {
return loop1;
}
node1 = node1.next;
}
// 没遇到loop2,说明不在一个环上,不相交返回null
return null;
}
}